土壤是具有高度异质性的复合体。早期的数字土壤制图研究主要关注水平方向的土壤空间变异和制图,对垂直方向空间变异和土壤三维制图考虑较少。近年来,三维地理信息技术和对地观测与探测技术的快速发展,极大地促进了土壤三维空间数据获取、三维空间推测、三维数据模型、三维模型构建和可视化方法等方面的研究。本文对三维空间土壤推测与土壤模型构建的已有方法进行梳理和评述,以期为三维数字土壤制图的应用和发展提供建议。以三维土壤制图、三维GIS、三维数据模型、三维地质建模、三维可视化、土壤空间变异、空间推测、克里格插值、土壤-景观分析、深度函数、机器学习、地统计学、随机模拟等为关键词检索Web of Science数据库,基于相关度、引用率和文献来源等因素进一步筛选出重点文献进行分析。归纳整理了土壤空间变异性、三维空间土壤推测、三维空间数据模型和三维模型构建等关键技术的现有研究体系,对各种三维推测和建模方法的优缺点和适用场景作出评价。针对目前研究中存在的垂直方向土壤数据稀少、土壤三维推测精度低、三维模型质量待提高等问题,提出一些可行的研究思路。
论文《三维空间土壤推测与土壤模型构建研究进展》发表在《土壤学报》,版权归《土壤学报》所有。本文来自网络平台,仅供参考。
关键词
三维空间;土壤空间变异性;土壤空间推测;三维数据模型;三维模型构建;数字土壤制图
引言
土壤是位于地球岩石圈、大气圈、水圈和生物圈交界部位的自然体,是人类赖以生存的重要生态系统服务提供者。制图是对土壤空间分布信息获取和表达的有效方式[1]。传统上,土壤类型图是通过野外土壤调查来获取区域内的土壤发生知识和分布规律,并将不同土壤类型的分布界线手工勾绘在地形图或遥感影像等地理底图上制作而成的;土壤属性图是以土壤类型图为基础图,根据相关的分析数据编制而成[2]。这些土壤图隐含了土壤调查专家对土壤空间分布与地理要素之间关系的认知知识。然而,传统土壤制图方法因成本高、效率低、制图周期长和制图质量不易量化评估等原因,难以满足数字时代自然资源管理、精准农业管理、环境污染防治和生态环境模拟等领域对高分辨率土壤空间分布数据的需求。随着地理空间分析、对地观测、统计学、数据科学以及相关领域的不断发展,数字土壤制图方法被广泛用于快速和低成本地推测土壤的空间分布。数字土壤制图又被称为预测性土壤制图(Predictive Soil Mapping, PSM),其主要制作方法是采用统计回归和机器学习等方法来构建土壤-景观关系的经验模型,或者基于土壤变量观测值间的空间自相关特征来构建空间统计模型,对土壤变量进行空间或时空推测,生成不同分辨率的土壤类型图或属性图,并进行不确定性分析[1,3]。
由于景观尺度上土壤的厚度远小于其在水平方向的延伸幅度,早期数字土壤制图研究大多集中在水平方向的土壤变异分析和预测性制图。然而,垂直方向的土壤变异分析具有重要的研究和应用价值。土壤在垂直方向上的变异一般大于水平变异,是评价土壤发育和划分土壤类型的主要依据[4-5]。此外,土壤垂直方向的变异信息对于从田块到区域尺度上的土壤过程模拟和土壤资源管理具有重要意义,是植物营养研究[6]、水文模拟[7]、土壤侵蚀研究[8]、滑坡预测[9]、关键带结构预测[10]、土壤污染修复[11]以及土壤碳储量估算[12]等研究所需要的关键数据。
近年来伴随着对地观测和近地传感等数据获取技术的迅速发展以及三维GIS时代的来临,二维数字土壤制图逐渐难以满足生产、科研等方面的需求,三维数字土壤制图技术日益受到关注和重视。本文从土壤空间变异的一般理论、三维空间土壤推测方法、三维空间土壤模型以及三维模型的构建方法等方面来阐述三维数字土壤制图的研究动态,并进一步讨论其发展趋势。
1 土壤空间变异的一般理论
1.1 区域化变量理论
土壤是十分复杂的自然综合体,一般而言土壤变量的空间变异由两部分组成:一是可以根据土壤形成因素来解释的结构性趋势变化,二是无法解释的局部随机性变化[13]。土壤变量遵循地质统计学方法中的区域化变量特征,其空间变异程度可以采用协方差函数和变差函数来表征。变差函数的计算公式为:
式中,(N(h))为空间距离(步长)为(h)的样本点对数目,(z_x)和(z_{x+h})为空间中点(x)与(x+h)处的土壤变量观测值。通常变差函数的值先随距离(h)的增大而快速增长,但当(h)达到一定值后,变差函数值增长减缓并趋于平稳。利用不同距离(h)与变差函数值的关系,可拟合出理论变差函数曲线,从而获得变程、块金值和基台值等参数,以表征空间变量的结构性和随机性特征。
土壤变量在三维空间的不同方向上和不同范围内常常呈现出不同的变异性。变差函数中的距离(h)是一个矢量,其方向和步长均是变化的。可以通过计算拟合垂直方向和水平各方向的变差函数来研究目标变量的异向性空间结构特征,并将不同方向上和不同范围内的多个变差函数套购组合为一个综合变差函数,以实现顾及各向异性的三维空间分布推测[14-15]。
1.2 分形理论
由于土壤的空间变异是各个成土因素在不同空间和时间尺度上作用和相互作用的产物,其结构性变异与随机性变异之间的区别在很大程度上取决于观测尺度。通常,在一个观测尺度上被认为是随机性的变异,在更大尺度上被认为是结构性的。为解决上述问题,Burrough[16]将分形理论应用于土壤空间变异研究,将一系列变差函数值(gamma(h))和对应的距离(h)绘制到双对数坐标上,并用最小二乘法拟合得到(log gamma(h))和(log h)之间的回归直线斜率(m)。土壤变量的变差函数分形维数(D)可用下式计算:
变差函数分形维数(D)表征了土壤变量的远程变异来源与短程变异来源之间的相对平衡,可量化对比不同土壤变量的空间变异特性。(D)值越小,土壤变量的结构性变异越强;(D)值越大,土壤变量的随机性变异越强。Burrough[17]还发现,当土壤空间变异是由具有不同权重和独立作用的土壤过程叠加造成时,非布朗分形模型可以提供不同变异来源的尺度和相对重要性的有用信息。但是,现实中由于各种成土因素在不同时空尺度上的交互作用以及大量随机过程的影响,土壤的形成与演化往往呈现出长期性和多期性。这导致土壤变量可能在不同时空尺度上具有不同的分布不均匀性和奇异性。多重分形方法通过谱函数来描述分形结构上不同局域条件或演化过程中不同层次所导致的特殊结构行为与特征,能够较好地描述土壤变量空间变异的复杂程度、不规则程度以及不均匀程度[18-19]。多重分形相较于单一分形能更全面地反映土壤属性在空间上高低起伏的分布特征,其经典计算方法主要为Rényi法和配分函数法。多重分形方法常用的工具是奇异性指数(alpha(q))和支持这个指数的分形子集的分形维数(f(q)):
式中,(delta)代表尺度;(n)代表当尺度为(delta)时的样本数量;(mu_i(delta))为概率质量;(q)为(mu_i(delta))的统计矩的阶;(alpha(q))为奇异性指数;(f(q))为(alpha(q))的分形子集的分形维数。Eghball等[20]对以上参数计算已做详细说明,这里不再赘述。(f(q))与(alpha(q))的关系曲线即为多重分形谱,其形状反映土壤变量空间变异特征。多重分形谱参数可为土壤变量在不同尺度间的空间插值转换提供指导依据。
2 三维空间土壤推测
2.1 土壤空间推测的基本方法
土壤空间推测是利用有限个已知样点的目标土壤变量数据和各种数学方法,来推测一定地理空间范围内各位置处的目标土壤变量数值。朱阿兴等[1]将其实现方法归纳为三大类:基于空间自相关的推测、基于要素相关性的推测以及基于空间自相关和要素相关性相结合的推测。
在较小研究区域上常用的土壤空间推测方法是基于空间自相关的推测。其中,应用较为广泛的有以反距离加权法为代表的确定性插值方法和以克里格插值法为代表的地统计方法。反距离加权法仅根据未知点与已知点之间的空间距离来确定权重进行加权平均插值,距未知点越近的样本点其权重越大。该方法简单易用,但对样本分布密度要求较高,否则插值精度较低。克里格插值法以变差函数分析为基础,在局部有限区域内对空间变量进行线性无偏最优估计。普通克里格插值法的推测公式如下:
式中,(z_0)为未知点的目标变量估值;(z_i)为第(i)个已知点的目标变量值;(lambda_i)为第(i)个已知点的权重,取决于目标变量的空间相关性。克里格插值法要求空间变量满足二阶平稳假设,其推测精度往往有赖于样点的代表性以及密度。
随着研究范围的扩大,影响土壤形成过程的因素增加,样本数据往往难以满足平稳假设。因此,研究者们常常采用基于要素相关性的空间推测方法,即基于所建立的土壤–景观统计模型来推测目标土壤变量的空间分布。Dokuchaev[21]提出的土壤发生学理论揭示了地理环境变量与土壤变量的关系。Jenny[22]将其发展为经验公式:(S=f(cl, o, r, p, t, ...))(其中,S代表土壤,cl、o、r、p、t分别代表气候、生物、地形、母质和时间),为定量研究土壤变量与地理环境变量之间的关系提供了理论依据。随着计算机和对地观测技术的迅猛发展,地理信息系统、全球定位系统、数字高程模型、遥感和近地传感为土壤空间推测提供了强大的推理工具和数量众多的数据源。在此背景下,McBratney等[23]提出了新的一般性公式:(S=f(s, c, o, r, p, a, n ...))(其中,S为待推测点的目标土壤变量,如土壤类型或土壤理化属性;s、c、o、r、p、a、n分别表示该点的其他土壤变量以及气候、生物、地形、母质、时间、空间等变量)。为描述三维空间土壤变量与环境变量的动态关系,Grunwald等[24]提出了STEP-AWBH模型:
式中,(SA)代表土壤目标变量;S、T、E、P分别代表相对“静态”的土壤、地形、生态和母质变量;A、W、B、H分别代表相对“动态”的大气、水、生物和人为变量;j是每个因素中变量的数量;(p_x)代表在地球特定位置上空间分辨率为x的像素;(t_c)代表当前时间;(t_i)代表过去到当前的时间间隔;z代表深度。上述这些土壤-景观关系模型中的(f())是指基于实测数据推断得到的表达目标变量和环境变量之间定量关联关系的经验函数,其推断方法有统计学方法、机器学习与数据挖掘方法、基于专家知识的方法以及基于样点代表性的方法等[1]。
基于空间自相关和要素相关性相结合的土壤空间推测是指同时考虑目标土壤变量的空间自相关性和目标变量与环境变量之间的统计相关性来推测目标变量的空间分布。其代表性方法包括协同克里格插值法、回归克里格插值法和地理加权回归等。协同克里格法本质上是一种广义空间线性模型[23]。它使用协同区域化线性模型(Linear Model of Coregionalization, LMC)来结合目标变量和协同变量的变差函数与交叉协方差函数,建立并求解协同克里格方程组来确定线性估值中的权重系数,以使目标变量的估计方差最小。因此,它是平稳假设下的一种最优无偏线性插值方法。回归克里格法是将目标土壤变量与环境变量回归的残差项进行克里格插值并与回归模型推测值相加,得到目标变量的空间推测结果[25]。这是一种在空间非平稳条件下的无偏线性插值方法。地理加权回归也是非平稳条件下的一种推测方法,其逐点建立局部加权回归方程,基于采样点到回归点的空间位置距离来设置不同采样点上各回归参数的权重函数[26]。空间自相关与要素相关结合的空间推测方法,在一定程度上能提高空间推测精度。然而,其缺点是对样本数量与分布要求较高,即要求样本同时满足平稳假设和要素相关性稳定[27]。
2.2 三维空间土壤推测方法
三维空间内土壤推测的实现方法可分为分层二维推测和三维推测。
2.2.1 分层二维推测
分层二维推测是将三维空间划分为多个水平或垂直方向的二维空间,分别在每一个二维空间上对离散数据进行插值或拟合,组合多个二维空间插值结果来实现三维空间推测。目前在三维土壤制图领域,研究者们多是根据样点剖面观测数据找到合适的土壤深度函数来描述目标土壤变量在垂直方向上的变化,估算出任意深度的样点土壤变量值,再基于每一深度的样点土壤变量值分别进行水平方向空间推测[28],由此实现对三维空间中每一位置处的土壤变量推测。
土壤深度函数是描述土壤变量在垂直方向上随深度变化的函数。Jenny[22]指出每一种土壤属性均有自己的垂直分布模式或特定的“深度函数”。常用的土壤深度函数模型有指数函数、幂函数、多项式函数以及样条函数等[29]。指数函数与幂函数适用于描述单调变化,多项式及样条函数可用于描述非单调变化。样条函数实质是一种分段多项式函数,其灵活性较高,目前被广泛用于模拟各种土壤变量的垂直方向分布。在人类对土壤有强烈影响或者土壤剖面中存在高度差异土层的地区,土壤变量的深度分布可能同时呈现出连续和不连续的变化特征[30]。对于这类土壤,简单的指数、幂、多项式等函数模型不再适用。研究者采用针对性的土壤深度函数来推测特定土壤变量的垂向变化。Kempen等[30]基于经验确定不同类型发生层的有机质深度函数,通过组合各发生层深度函数来描述不同土壤类型的剖面有机质深度变化。Li等[31]利用线性模型和Tikhonov正则化函数模拟浙江杭州湾盐碱地水田田块的土壤电导率深度变化。针对特定地区或特定土壤属性建立的深度函数,其拟合能力较强,但迁移和泛化能力不强。
分层二维推测是目前三维土壤制图中应用最为广泛的一类方法。Veronesi等[32]在绘制田块尺度土壤压实度的三维分布图时,利用多项式函数拟合压实度随深度下降的变化,采用普通克里格插值法进行水平方向空间推测。Malone等[33]、Liu等[29]和赵彦锋等[34]利用等积二次样条函数模拟土壤碳的垂直变化,采用神经网络、径向基函数、分位数随机森林等算法来推测区域尺度土壤碳的水平方向分布。Song等[12]采用指数函数和幂函数模拟垂直方向不同深度区间土壤有机碳的变化,使用地理加权回归算法推测有机碳的水平方向分布。分层二维推测是一种相对容易实现的三维空间推测方法,对土壤变量的推测成果通常是用不同深度的土壤变量水平方向分布图(切片)来展示。但是,该类方法可能会导致目标土壤变量的垂直与水平空间变化之间存在一定割裂[28],不能准确反映三维空间内目标变量的真实分布。因此,其推测成果并非真正意义的三维表示,难以直接支持三维空间分析。
2.2.2 三维推测
三维推测是将三维空间进行规则或不规则网格体剖分后,使用已知样点剖面数据和各类插值拟合方法推测出网格体中心点或顶点的目标变量数值。常见方法有以下几种:
1. 三维确定性插值:代表方法是三维反距离加权插值。研究者们使用该方法推测田块尺度(韩霁昌等[35]、云安萍等[36]和李洪义等[37])或区域尺度[38]的土壤盐分三维空间分布。该方法的优点在于简单和不受维度限制,但是预测精度依赖于样本分布密度,而且未考虑样点的三维空间结构特征。有学者提出了一种顾及空间异向性的局部径向基函数三维空间插值方法[15],其基于不同方向的变异函数分析来设置局部搜索椭球体进行局部线性加权插值。然而,该方法求算较为复杂,对样本数据要求更高。
2. 三维克里格插值:该类方法考虑了目标土壤变量的三维空间变化特征,分别计算和拟合不同特征方向的变异函数,通过套构组合得到综合变异函数模型,用于三维空间的克里格插值计算。徐丹等[39]在模拟河南新郑市农田土壤有机质和全氮三维空间分布特征时,发现三维普通克里格插值较三维反距离加权插值的精度更高。Chen等[40]在进行河北曲周县土壤有机质三维制图时,对土壤有机质经深度函数拟合后的残差进行三维普通克里格插值,以实现对土壤有机质的三维推测。
为解决普通克里格插值在目标变量样本稀疏时推测精度较低的问题,回归克里格插值和协同克里格插值被应用于土壤三维空间推测。回归克里格法对待测点的估值是目标变量与辅助变量多元回归结果与对回归残差进行克里格插值结果的加和。因此在目标变量样本较少时,选用样本较多且与目标变量相关性较强的辅助变量能得到较普通克里格法更为精确的推测结果[41]。Zhang等[42]通过将三维回归克里格插值与伽马射线光谱和土壤表观电导率等土壤近地传感技术相结合,绘制了加拿大麦吉尔大学实验农场的土壤含水量、有机质和黏粒等属性的三维分布图。回归克里格法能提高推测精度,且一定程度上解决了三维普通克里格插值的过度平滑问题[43]。然而,在辅助变量样本较少或者与目标变量相关性不强时,其推测精度未必好于普通克里格法[44]。协同克里格法将两个或多个具有显著相关性的区域化变量联合考虑,通过计算拟合目标变量和协同变量的自协方差函数和交互协方差函数来求解协同克里格方程组得到权重系数进行空间插值。Gallichand等[45]曾对比了三维普通克里格、三维泛克里格、三维普通协同克里格和三维泛协同克里格等方法推测田块尺度土壤电导率和钠吸附比的三维空间分布精度,发现三维普通协同克里格法的推测精度均较高。由于交互协方差函数的计算繁琐以及在一些待估测点存在协同克里格方程组呈现病态而导致目标变量无解的情形,因此在样本数据较多的情况下,学者们一般采用同位协同克里格法进行三维空间推测。同位协同克里格法不需要求解协同克里格方程组,其插值结果等价于目标变量克里格估值与同位协变量克里格估值的简单加权混合[46]。三维协同克里格法能够将稀疏的目标土壤变量剖面数据与易获取的协同变量数据如土壤近地传感数据进行一体化综合,以提高目标变量的推测精度。
三维克里格方法充分考虑目标变量的空间自相关特性,采用变差函数描述变量的空间异质性,并利用克里格方差估计给出推测值的不确定性,便于估计推测结果的可靠性。由于以上优点,三维克里格方法在田块和区域尺度土壤变量三维推测中均有应用。但是,三维克里格方法通常需要样本密度较高以呈现三维空间内土壤变量的空间结构性。
3. 多点地统计插值:传统地质统计学中所采用的变差函数仅能表征两点间的空间相关性,难以表达具有复杂形态的地质体[47]。为解决这一问题,考虑了空间相关性以及多个属性之间复杂关系的多点地质统计学应运而生[48]。多点地质统计学用“训练图像”代替变差函数,在每个待估点使用重新扫描训练图像的方法来获得局部条件概率,并应用序贯指示模拟方法产生模拟实现。Strebelle[49]提出的单正态方程模拟是多点地质统计学中最具代表性的方法。Meerschman等[50]首次将多点地质统计插值方法应用于土壤领域。Zhou等[51]提出了一种基于知识的多点统计(Knowledge-based multiple-point statistics, KMPS)方法来模拟地基土体的异质性和空间趋势,结果表明在勘探钻孔数据稀少的情况下,该方法能有效地推测不同类型地基土层的空间分布。多点地质统计学要求训练图像平稳,即训练图像内目标体的几何构型及目标形态在全区基本不变。虽然已有学者提出将非平稳的训练图像转换为平稳训练图像的方法,但是对于无规律的局部明显变异性,目前尚缺乏有效的解决方案[47]。
4. 分形地统计插值:分形地统计插值是将分形与地统计学方法相结合的空间插值方法。Cheng[52]于1999年提出了基于多重分形谱奇异性指数的空间插值模型。该模型将数据分解为奇异成分和非奇异成分,前者用局部奇异指数表征邻域值的凹凸特性,从多重分形的角度量化测量的缩放不变性;后者是平滑成分,使用普通克里格或其他移动平均模型进行估算:
式中,(Z(x_0))为(x_0)位置点属性值;(a(x_0))为(x_0)处属性值奇异性指数;(Omega(x_0, varepsilon))为以(x_0)为中心、(varepsilon)为半径的滑动窗口;(omega(|x_0 - x_i|))为空间插值中已知点属性值(Z(x_i))的加权函数,(omega)的选择可以是空间插值方法的任何一种,如克里格插值或距离反比法等。与传统的地统计学插值法相比,分形地统计插值能更好地捕捉空间变量的多尺度特征,适用于土壤这类复杂和非线性系统。但是,分形理论的应用前提是空间变量具有分形特征,对于某些不具有自相似性或尺度不变性的目标土壤属性,该类插值方法的应用效果不理想。
5. 随机模拟方法:由于传统的克里格插值方法本质上是基于已知点数据进行加权移动平均来推测未知点数据,具有平滑效应。为较好地刻画目标变量空间分布的非均匀性和不确定性,尽可能接近真实空间分布,学者们采用随机模拟方法,将空间场视为非平稳和非均匀的,通过建立属性场的概率模型,获取可能的概率实现结果。常用的随机模拟方法有序贯条件模拟和转移概率地统计学模拟。序贯条件模拟主要包含序贯高斯模拟和序贯指示模拟:序贯高斯模拟适用于连续型变量,按Monto-Carlo算法根据条件概率密度函数随机取值,能保持全局的空间变异强度,并能对未采样的空间位置提供任意多个同等可能性的实现来度量不确定性[53];序贯指示模拟将指示克里格与序贯模拟相结合,适用于类型变量[54]。姚荣江等[55]利用序贯高斯模拟法进行苏北沿海滩涂田块尺度上的土壤盐分三维空间分布推测。He等[56]利用序贯指示模拟法进行中国农业大学曲周实验站(15 km^2)范围的土壤容重三维分布推测。由于序贯模拟算法每个未取样点仅推测一次,已推测的样点被看做采样点参加下一次模拟,这可能导致推测结果的连续性较差[47]。基于Markov链的地统计学方法使用转移概率矩阵来描述区域变量的空间变异性,能较好地描述土壤属性的空间分布连续性。贺勇等[57]与王伟鹏等[58]运用Markov链地统计学方法进行田块和县域尺度上土壤质地的三维空间分布推测。但由于该类方法属于迭代方法,受到迭代收敛的局限,其应用也受到了限制[59]。
三维推测方法通常对样本密度以及样本代表性具有一定要求,现阶段在田块尺度上应用较多,在区域尺度上应用较少。但是,三维推测同时考虑目标土壤变量在水平和垂直方向上的变化特征,计算得到的土壤三维属性场数据通常能够支持三维空间运算。因此,虽然目前该类方法的推测精度并不一定高于分层二维推测方法,但毫无疑问是土壤三维空间模拟今后的研究重点之一。
3 三维空间土壤模型构建
三维空间土壤模型构建,主要包括三维空间土壤数据模型(即三维空间土壤模型的数据结构)和三维空间土壤模型的建模方法两部分。前者是对三维土壤空间中土壤对象的抽象和模拟表达,包括数据逻辑组织、操作方法以及规则约束条件等内容;而后者则是针对特定的数据模型,利用土壤图、样点剖面和区域截面等土壤数据构建一定区域内三维空间土壤模型的算法。所构建的三维空间土壤模型主要用于三维场景可视化展示和三维空间分析。
3.1 三维空间土壤数据模型
到目前为止,国内外学者提出了几十种三维空间数据模型,其中代表性的有三十余种。吴立新等[60]将三维空间数据模型分为面模型、体模型、混合模型与集成模型;Gong等[61]则将三维空间数据模型归类为基于表面的模型、基于体的模型以及混合模型。根据数据模型中基本要素的维度,李安波等[62]将三维空间数据模型划分为点集模型、线框模型、表面模型、实体模型、体元模型和混合模型六类。
针对土壤三维建模的应用特点,本文在借鉴前述分类方法的基础上,采用了“应用+数据结构”的层次化分类方法进行论述。为全面表达三维空间中土壤实体对象的几何形态和内部属性的数据特征,首先需要分别从要素的视角和场的视角[63]来建立三维空间土壤数据模型。前者用于界定不同土壤实体对象的空间范围以及表达土体的空间结构,通常称为土壤三维几何对象模型;后者则用于表达土体物理、化学或生物等属性在三维空间中的连续变化,通常称为土壤属性场模型。
3.1.1 土壤三维几何对象模型
考虑到三维土体模型的展示效率和空间分析需求,适用于土体对象三维几何形态表达的数据模型主要包括点集模型、线框模型、表面模型和实体模型。
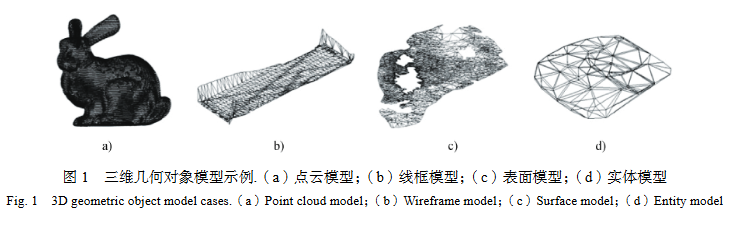
点集模型,又称为点云模型(Point Cloud Model,图1a),其基本思想是采用大量的三维点集合描述对象的表面。点云数据可由三维激光扫描仪器高效、高精度地采集获取。然而,点云间由于缺乏必要的拓扑邻接信息,无法直接支持土壤空间分析、虚拟现实碰撞检测等功能。目前,基于点云数据的相关应用主要包括土壤表面的精确重建[64]、粗糙度测量[65]、坡面侵蚀检测[66]等。
线框模型(Wireframe Model,图1b)与表面模型(Surface Model,图1c)作为实体模型出现前的过渡模型,主要具有结构简单和易于理解等优点。然而,线框模型缺乏表示复杂曲面和实体的能力,而表面模型则无法明确定义形体究竟存在于表面的哪一侧[62]。因此,在具体的三维模型构建中,这两种模型的应用相对较少,并很快被实体模型所取代。
实体模型(Entity Model)主要通过组成该几何体的边界面所形成的半空间来表示一个对象,其内部属性被假设为相同的[62]。实体模型侧重于对象表面几何形体的表达,即更多地用于描述不同几何对象的空间分布与几何形态。Grunwald等[67]使用虚拟现实建模语言(Virtual Reality Modeling Language, VRML)构建了土体、聚合土体、土链和区域四种尺度上的土壤发生层三维实体模型。Santos等[68]在分析瑞士Sarine冲积平原土壤三维空间变异性时,以样点剖面的各土层深度为顶点逐层构建不规则三角网(Triangular Irregular Network, TIN),并将其缝合成实体模型。实体模型是使用最广泛的三维几何对象模型,包括边界表示模型(Boundary Representation Model, B-Rep)、多层DEM模型、三维拓扑数据模型、形式化三维数据结构模型、简化空间模型等[62]。B-Rep模型是最为常见的实体模型(图1d),通过顶点、边、面片及它们之间的拓扑关系描述实体,并通过面片的法向量确定模型的内外侧[62]。虽然B-Rep模型可以使用精细的面片来表达空间分布复杂的土壤对象表面,但不适用于表达土壤理化性质的三维空间连续分布特征。
3.1.2 土壤属性场模型
土壤属性场模型是以体元模型(Volume Model)为载体,采用三维空间插值方法进行体元赋值,用于表达非均质、连续变化的土壤属性三维空间分布特征的模型。体元模型的核心思想是将三维实体分割成内部同质的三维块体,并将每一块体中心位置的属性赋予相应块体,从而得到相应的体元模型。体元模型可以分为规则体元模型(图2)和不规则体元模型(图3),后者在三个方向上体元的尺寸不相等且不为常数。
规则体元模型主要包括体素模型[69](图2a)、八叉树模型[70](图2b)、针体模型[71](图2c)和规则块体模型[69](图2d)。在土壤属性三维模型构建应用中,规则体元模型由于其构建方法简单而得到广泛应用。基于电磁感应反演的表观土壤电导率数据和反距离加权插值、协同克里格插值等空间推测方法,吴亚坤等[38]、Li等[31]和韩霁昌等[35]使用规则块体数据模型分别构建了新疆典型绿洲区、浙江杭州湾盐碱地水田田块和陕西关中卤泊滩典型田块的土壤盐分三维模型。
虽然规则体元模型数据结构简单、规律性强且易于实现,但其描述地表起伏变化的能力相对较弱。尽管可以通过降低体元尺寸的方法来改善这一问题,但这会导致空间单元数目以及数据量呈三次方增长[72]。不规则体元模型较好地克服了这一缺点。不规则体元模型主要包括四面体模型[73](图3a)、金字塔模型[74](图3b)、三棱柱模型[69](图3c)、广义三棱柱模型[75](图3d)、非规则块体模型(图3e)等。虽然不规则体元模型的结构相对于规则体元模型而言更加复杂,但其优势在于能够根据土壤实体的形态进行模型构建,从而提高土壤属性场模型的构建精度。目前,尚未检索到不规则体元模型在土壤三维模型构建中的应用,但将其引入土壤三维模型构建是必要和有意义的。
此外,切片模型(Brus[44];Meersmans[76];Taghizadeh-Mehrjardi[77];Heitkamp[78])由于能较好地表达土壤属性在三维空间上的分布状况,也有较多应用。切片模型指的是三维模型中不同深度上切面的二维投影。对于土壤属性而言,切片模型的每个切片实际上是表达对应深度土壤性质分布的二维土壤栅格地图,严格而言切片模型并不能归为三维模型。
3.2 三维空间土壤模型的建模方法
根据数据模型以及模型构建数据源的不同,下面分别从土壤三维几何模型构建和土壤属性场模型构建两个方面进行论述。
3.2.1 土壤三维几何对象模型构建方法
基于B-Rep模型的广泛应用和强大空间分析支持能力,本节主要针对B-Rep模型论述有关的土壤三维几何对象模型构建方法。此外,针对不同的数据源进行三维建模时,由于具有不同的数据结构和建模流程,需要研究不同的算法。
1. 基于点位剖面的土壤三维几何模型构建:土壤发生层与地层的空间结构相似,点位土壤剖面的数据结构也与地质钻孔基本一致。在地学领域,目前可以利用钻孔数据构建具有复杂地质构造(断层、褶皱等)和复杂空间形态(地层尖灭、透镜体等)的精细三维模型[79]。黄键初[80]将基于钻孔数据构建三维地质体模型的方法应用于土壤三维几何对象模型的构建,取得了较好的建模效果。
土壤三维几何对象模型的建模质量主要受到点位土壤剖面密度的影响。土壤剖面数据获取上的困难,决定了点位土壤剖面数据的稀疏特性。因此需要对其进行加密处理,以保障模型的建模质量。土壤剖面的加密实质上是在稀疏位置,基于前述的三维空间土壤推测方法,利用地理相似性定律[81]或空间插值原理,推断土壤各发生层顶底界面的高程属性,从而在加密位置生成虚拟点位土壤剖面。
基于点位剖面数据构建土壤三维几何模型的一般步骤如图4所示。首先,在数据稀疏位置利用三维空间土壤推测方法生成加密虚拟剖面;其次,采用Shen等[82]提出的方法,在土壤剖面之间的发生层尖灭位置生成虚拟剖面,以控制尖灭位置的发生层空间形态;最后,结合实测和虚拟生成的点位土壤剖面信息,逐层构建土壤发生层的上下表面三角网,并进行表面缝合处理,从而得到土壤发生层实体的三维几何对象模型。
2. 基于区域截面的土壤三维几何模型构建:区域土壤截面与地质剖面均反映了一定范围内土壤发生层或地层的分布状况与变化情况。基于地质剖面进行三维地质模型构建的方法已相对成熟。同理,区域土壤截面亦可用于土壤三维几何对象模型的构建。基于区域土壤截面进行三维模型构建的关键在于对土壤截面间发生层轮廓的对应。传统的基于轮廓线的连接算法主要适用于单体建模。但在区域土壤截面中由于各个发生层相互邻接,轮廓线算法不能直接应用于基于区域土壤截面的三维模型构建中。屈红刚等[83]提出了一种适合于地质剖面中多个邻接地质实体的三维模型构建方法,为区域土壤截面中发生层的轮廓线连接方法提供了基本思路。基于这一思路,黄键初[80]将实测区域土壤截面与虚拟土壤截面作为数据源,进行了基于土壤截面的土壤三维几何对象模型构建方法研究(图5)。
土壤截面数据的利用为土壤三维几何对象模型的构建提供了一种思路。但是由于区域断面数据非常稀疏,其模型精度尚难以满足应用需要。今后,基于土壤发生学知识推断虚拟土壤截面的方法应进一步加强[84],以改善数据过于稀疏的制约。
目前基于样点土壤剖面或基于区域土壤截面的三维几何模型构建方法[79]均使用了单一数据源。然而,在地质体三维模型构建领域已经证明多源数据的应用可以有效提高模型精度[85]。因此,融合点位土壤剖面、区域土壤截面、土壤图等多源数据进行土壤三维几何对象模型构建,将成为今后土壤三维几何对象模型构建的研究重点。
针对三维几何对象模型中常见的尖棱、不平滑等问题,一些学者已经尝试利用隐式建模方法进行解决[86]。隐式建模是指利用隐式函数来表达三维实体表面。土壤三维几何模型构建方法中同样具有所建模型存在尖棱、不平滑等问题,引入隐式建模方法来优化土壤三维几何对象模型具有一定的研究价值。
3.2.2 土壤属性场模型构建方法
土壤三维属性场模型构建通常采用相对简单的规则体元模型。基于样点剖面数据来构建土壤三维属性场模型,主要包括两个环节:一是基于研究区域的三维空间范围剖分生成体元模型;二是基于样点剖面数据进行空间插值以推测三维空间中任意点的土壤理化属性值,并将这些数值赋予对应的体元。对于形态相对简单的建模区域,可通过空间范围约束简单剖分生成体元模型;而对于形态复杂的建模区域,则需要在土壤三维几何对象模型的基础上,通过空间离散方法生成精细体元模型。
构建规则体元三维空间土壤属性场模型的方法相对简单,所生成的模型能够方便地支持空间分析和在数字地球平台(如Google Earth、Censium等)中展示。然而,今后需加强不规则体元模型构建方法的研究,以提高对复杂土壤属性空间分布的表达能力。
4 总结与展望
近年来,土壤的三维空间推测方法以及三维模型构建方法取得了飞速的进展。本节针对目前研究中存在的垂直方向土壤数据稀少、土壤三维空间推测精度低、三维数据模型质量有待提高等问题,提出了一些可行的研究思路,做出了如下展望:
1. 综合应用各种土壤剖面信息快速采集技术。三维空间土壤推测和数据模型构建的主要制约在于垂直方向的土壤数据不充足。通过人工挖掘采样和实验室分析等传统手段来获取土壤剖面信息费时费力,获取的数据量少且空间分布不均。原位土壤光谱、探地雷达和电磁感应等光电传感探测技术具有快速和低成本等优势[87],但存在不确定性较高、各种方法所获取数据融合度低等问题。应加强多种近地传感技术的融合应用研究,以获取更高质量的土壤剖面信息。
2. 探索使用数据增强和深度迁移学习等技术来克服剖面数据不足问题。剖面数据不足和数据集偏差问题使大尺度上三维土壤推测和数据模型的精度十分受限。应加强土壤知识与人工智能方法的结合应用,例如,使用土壤过程模型来模拟表层土壤属性与深层土壤属性之间的关系,利用深度学习建立遥感等数据源与表层土壤属性之间的关系,将深度学习模型的输出作为土壤过程模型的输入以获取深层土壤属性信息;使用地理相似性等理论模拟和合成适量的虚拟剖面数据。
3. 针对不同尺度和应用场景选择适配的三维空间推测方法。三维空间推测是将有限数量的离散观测值推广至整个研究区域三维空间的过程。首先需要考虑土壤空间异质性和尺度效应,根据研究尺度、数据性质、计算资源以及对推测结果的精度要求,选择合适的三维空间推测方法。针对小尺度研究,克里格插值可能是一个合适的选择,尤其是在具有均匀样本分布的区域,对于空间关系复杂、具有足够密集观测样本的区域,也可以考虑机器学习方法如随机森林或支持向量机;针对中等尺度研究,机器学习方法如随机森林、神经网络或深度学习技术可能更为适用,这些方法可以更好地处理中等尺度上的复杂性和非线性关系。
4. 加强三维土壤模拟的不确定分析与质量控制。不同三维数据模型的适应性各不相同,首先要根据具体三维数据模型构建目的来选择合适的三维空间数据模型。针对三维几何对象模型,优化策略包括:融合土壤剖面、区域土壤断面和土壤图等多源异构数据进行土壤三维模型构建;基于隐式建模方法解决三维模型中尖棱、过度不平滑等问题。针对三维属性场模型,优化策略包括:对于规则体元模型,引入地形信息进行土壤三维属性场模型的优化;对于不规则体元模型,可以根据土壤实体几何形态进行构建。
5. 加强土壤三维数据模型的规范化。基于通用、规范的土壤三维数据模型,既可以提高土壤三维模型与其他地学三维模型的有机融合与空间分析能力,也可以支持将土壤三维模型投放至三维数字地球平台上进行直观、形象的展示和应用。
参考文献
[1] 朱阿兴,杨琳,樊乃卿,等. 数字土壤制图研究综述与展望[J]. 地理科学进展,2018,37(1):66-78.
[2] 李锦. 小比例尺土壤制图理论和方法的研究[J]. 土壤学报,1988,25(4):336-348.
[3] Hengl T, MacMillan R A. Predictive soil mapping with R[M]. Netherlands: Wageningen, 2019.
[4] 张甘霖,朱阿兴,史舟,等. 土壤地理学的进展与展望[J]. 地理科学进展,2018,37(1):57-65.
[5] Hartemink A E, Zhang Y, Bockheim J, et al. Soil horizon variation: A review[J]. Advances in Agronomy, 2020, 160: 125-185.
[6] Parker R S. Absorption, metabolism, and transport of carotenoids[J]. FASEB Journal: Official Publication of the Federation of American Societies for Experimental Biology, 1996, 10(5): 542-551.
[7] Pelletier J D, Rasmussen C. Geomorphically based predictive mapping of soil thickness in upland watersheds[J]. Water Resources Research, 2009, 45(9): w09417.
[8] Mehnatkesh A, Ayoubi S, Jalalian A, et al. Relationships between soil depth and terrain attributes in a semi arid hilly region in western Iran[J]. Journal of Mountain Science, 2013, 10(1): 163-172.
[9] Ho M H, Chan C M. Some mechanical properties of cement stabilized Malaysian soft clay[J]. International Journal of Civil and Environmental Engineering, 2011, 5(2): 76-83.
[10] Tye A M, Kessler H, Ambrose K, et al. Using integrated near-surface geophysical surveys to aid mapping and interpretation of geology in an alluvial landscape within a 3D soil-geology framework[J]. Near Surface Geophysics, 2011, 9(1): 15-31.
[11] 陶欢,廖晓勇,曹红英,等. 场地土壤污染物含量三维刻画的研究进展[J]. 地理学报,2022,77(3):559-573.
[12] Song X D, Wu H Y, Liu F, et al. Three-dimensional mapping of organic carbon using piecewise depth functions in the red soil critical zone observatory[J]. Soil Science Society of America Journal, 2019, 83(3): 687-696.
[13] Wilding L P, Drees L R. Spatial variability: A pedologist’s viewpoint1[J]. Diversity of Soils in the Tropics, 1978, 34: 1-12.
[14] 宋春华,崇仁杰,程立芝. 地质统计学储层建模技术在印尼马六甲AI和N油田的应用[J]. 中国海上油气(地质),2001,15(5):340-344,360.
[15] 段平,盛业华,张思阳,等. 顾及异向性的局部径向基函数三维空间插值[J]. 武汉大学学报(信息科学版),2015,40(5):632-637.
[16] Burrough P A. Multiscale sources of spatial variation in soil. I. The application of fractal concepts to nested levels of soil variation[J]. Journal of Soil Science, 1983, 34(3): 577-597.
[17] Burrough P A. Multiscale sources of spatial variation in soil. II. A non-Brownian fractal model and its application in soil survey[J]. Journal of Soil Science, 1983, 34(3): 599-620.
[18] Kravchenko A N, Boast C W, Bullock D G. Multifractal analysis of soil spatial variability[J]. Agronomy Journal, 1999, 91(6): 1033-1041.
[19] 张法升,刘作新. 分形理论及其在土壤空间变异研究中的应用[J]. 应用生态学报,2011,22(5):1351-1358.
[20] Eghball B, Schepers J S, Negahban M, et al. Spatial and temporal variability of soil nitrate and corn yield[J]. Agronomy Journal, 2003, 95(2): 339-346.
[21] Dokuchaev V V. Russian chernozem[M]. Jerusalem: Israel Program for Scientific Translations, 1967.
[22] Jenny H. Factors of soil formation: A system of quantitative pedology[M]. North Chelmsford: Courier Corporation, 1994.
[23] McBratney A B, Santos M L M, Minasny B. On digital soil mapping[J]. Geoderma, 2003, 117(1/2): 3-52.
[24] Grunwald S, Vasques G M, Rivero R G. Fusion of soil and remote sensing data to model soil properties[J]. Advances in Agronomy, 2015, 131: 1-109.
[25] Knotters M, Brus D J, Voshaar J H O. A comparison of kriging, co-kriging and kriging combined with regression for spatial interpolation of horizon depth with censored observations[J]. Geoderma, 1995, 67(3/4): 227-246.
[26] Brunsdon C, Fotheringham A S, Charlton M E. Geographically weighted regression: a method for exploring spatial nonstationarity[J]. Geographical Analysis, 1996, 28(4): 281-298.
[27] Hengl T, Gruber S, Shrestha D P. Reduction of errors in digital terrain parameters used in soil-landscape modelling[J]. International Journal of Applied Earth Observation and Geoinformation, 2004, 5(2): 97-112.
[28] Lai Y R, Orton T G, Pringle M J, et al. Increment-averaged kriging: A comparison with depth-harmonized mapping of soil exchangeable sodium percentage in a cropping region of eastern Australia[J]. Geoderma, 2020, 363: 114151.
[29] Liu F, Zhang G L, Sun Y J, et al. Mapping the three-dimensional distribution of soil organic matter across a subtropical hilly landscape[J]. Soil Science Society of America Journal, 2013, 77(4): 1241-1253.
[30] Kempen B, Brus D J, Stoorvogel J J. Three-dimensional mapping of soil organic matter content using soil type specific depth functions[J]. Geoderma, 2011, 162(1/2): 107-123.
[31] Li H Y, Shi Z, Webster R, et al. Mapping the three-dimensional variation of soil salinity in a rice-paddy soil[J]. Geoderma, 2013, 195: 31-41.
[32] Veronesi F, Corstanje R, Mayr T. Mapping soil compaction in 3D with depth functions[J]. Soil & Tillage Research, 2012, 124: 111-118.
[33] Malone B P, McBratney A B, Minasny B, et al. Mapping continuous depth functions of soil carbon storage and available water capacity[J]. Geoderma, 2009, 154(1/2): 138-152.
[34] 赵彦锋,李怡欣,马盼盼,等. 近30年河南省耕地土壤有机碳的三维变化与关键因素研究[J]. 土壤学报,2023,60(5):1409-1420.
[35] 韩霁昌,李晓明,孙剑虹,等. 卤泊滩典型田块土壤盐分三维空间分布研究[J]. 自然资源学报,2014,29(5):847-854.
[36] 云安萍,鞠正山,胡克林,等. 基于距离反比法的土壤盐分三维空间插值研究[J]. 农业机械学报,2015,46(12):148-156.
[37] 李洪义,顾呈剑,但承龙,等. 基于VRML的土壤电导率三维空间变异性虚拟现实建模研究[J]. 土壤学报,2015,52(4):776-782.
[38] 吴亚坤,刘广明,杨劲松,等. 基于反距离权重插值的土壤盐分三维分布解析方法[J]. 农业工程学报,2013,29(3):100-106.
[39] 徐丹,刘昌华,蔡太义,等. 农田土壤有机质和全氮三维空间分布特征研究[J]. 农业机械学报,2015,46(12):157-163.
[40] Chen C, Hu K L, Li H, et al. Three-dimensional mapping of soil organic carbon by combining Kriging method with profile depth function[J]. PLoS One, 2015, 10(6): e0129038.
[41] Zhu Q, Lin H S. Comparing ordinary Kriging and regression Kriging for soil properties in contrasting landscapes[J]. Pedosphere, 2010, 20(5): 594-606.
[42] Zhang Y K, Ji W J, Saurette D D, et al. Three-dimensional digital soil mapping of multiple soil properties at a field-scale using regression Kriging[J]. Geoderma, 2020, 366: 114253.
[43] Hengl T, Heuvelink G B M, Rossiter D G. About regression-Kriging: From equations to case studies[J]. Computers & Geosciences, 2007, 33(10): 1301-1315.
[44] Brus D J, Yang R M, Zhang G L. Three-dimensional geostatistical modeling of soil organic carbon: A case study in the Qilian Mountains, China[J]. Catena, 2016, 141: 46-55.
[45] Gallichand J, Buckland G D, Marcotte D, et al. Spatial interpolation of soil salinity and sodicity for a saline soil in Southern Alberta[J]. Canadian Journal of Soil Science, 1992, 72(4): 503-516.
[46] 李少华,张昌民,胡爱梅,等. 煤储层孔隙度的协同模拟[J]. 煤炭学报,2007,32(9):980-983.
[47] 吴胜和,李文克. 多点地质统计学--理论、应用与展望[J]. 古地理学报,2005,7(1):137-144.
[48] Matheron G. Principles of geostatistics[J]. Economic Geology, 1963, 58(8): 1246-1266.
[49] Strebelle S. Conditional simulation of complex geological structures using multiple-point statistics[J]. Mathematical Geology, 2002, 34(1): 1-21.
[50] Meerschman E, van Meirvenne M, van De Vijver E, et al. Mapping complex soil patterns with multiple-point geostatistics[J]. European Journal of Soil Science, 2013, 64(2): 183-191.
[51] Zhou X Q, Shi P X, Sheil B. Knowledge-based multiple point statistics for soil stratigraphy simulation[J]. Tunnelling and Underground Space Technology, 2024, 143: 105475.
[52] Cheng Q M. Multifractal interpolation[C]. Proceedings of the Fifth Annual Conference of the International Association for Mathematical Geology, 1999: 245-250.
[53] 郭飞,葛成,韩宇. 嵌入式马尔科夫链的地质属性建模与应用[J]. 地理与地理信息科学,2012,28(1):47-50.
[54] 赵彦锋,孙志英,陈杰. Kriging插值和序贯高斯条件模拟算法的对比分析[J]. 地球信息科学学报,2010,12(6):767-776.
[55] 姚荣江,杨劲松,赵秀芳,等. 沿海滩涂土壤盐分空间分布的三维随机模拟与不确定性评价[J]. 农业工程学报,2010,26(11):91-97.
[56] He Y, Hu K L, Chen D L, et al. Three dimensional spatial distribution modeling of soil texture under agricultural systems using a sequence indicator simulation algorithm[J]. Computers and Electronics in Agriculture, 2010, 71: S24-S31.
[57] 贺勇,胡克林,李卫东,等. 华北冲积平原区土壤剖面质地层次空间分布的三维随机模拟[J]. 土壤学报,2008,45(2):193-200.
[58] 王伟鹏,刘建立,李晓鹏. 基于转移概率的区域土壤三维随机模拟及其不确定性评价[J]. 土壤,2014,46(6):1121-1128.
[59] Caers J, Journel A. Stochastic reservoir simulation using neural networks trained on outcrop data[C]. SPE Annual Technical Conference and Exhibition, 1998: SPE-49026-MS.
[60] 吴立新,史文中,Christopher Gold. 3D GIS与3D GMS中的空间构模技术[J]. 地理与地理信息科学,2003,19(1):5-11.
[61] Gong J Y, Cheng P G, Wang Y D. Three-dimensional modeling and application in geological exploration engineering[J]. Computers & Geosciences, 2004, 30(4): 391-404.
[62] 李安波,周良辰,闾国年. 地质信息系统[M]. 北京:科学出版社,2013.
[63] 刘瑜,汪珂丽,邢潇月,等. 地理分析中的空间效应[J]. 地理学报,2023,78(3):517-531.
[64] 刘振,杨玮,李民赞,等. 基于Kinect相机的土壤表面三维点云配准方法[J]. 农业机械学报,2019,50(S1):144-149.
[65] 张田,周忠发,王玲玉,等. 基于无人机点云数据土壤粗糙度测量方法[J]. 自然资源遥感,2023,35(1):115-122.
[66] 张志伟. 近景摄影测量技术和三维激光扫描技术在坡面侵蚀过程中的应用[D]. 武汉:华中农业大学,2022.
[67] Grunwald S, Barak P, McSweeney K, et al. Soil landscape models at different scales portrayed in Virtual Reality Modeling Language[J]. Soil Science, 2000, 165(8): 598-615.
[68] Santos M M L, Guenat C, Bouzelboudjen M, et al. Three-dimensional GIS cartography applied to the study of the spatial variation of soil horizons in a Swiss floodplain[J]. Geoderma, 2000, 97(3/4): 351-366.
[69] Houlding S W. Spatial data types and structures // Houlding S W. 3D Geoscience Modeling: Computer Techniques for Geological Characterization[M]. Berlin, Heidelberg, Germany: Springer-Verlag, 1994: 71-86.
[70] Chen H H, Huang T S. A survey of construction and manipulation of octrees[J]. Computer Vision, Graphics, and Image Processing, 1988, 43(3): 409-431.
[71] Shi W Z, Yang B S, Li Q Q. An object-oriented data model for complex objects in three-dimensional geographical information systems[J]. International Journal of Geographical Information Science, 2003, 17(5): 411-430.
[72] Houlding S. 3D geoscience modeling: Computer techniques for geological characterization[M]. New York: Springer Science & Business Media, 2012.
[73] Joe B. Construction of three-dimensional Delaunay triangulations using local transformations[J]. Computer Aided Geometric Design, 1991, 8(2): 123-142.
[74] 周良辰. 基于胞腔复形的三维空间数据模型及分析方法研究[D]. 南京:南京师范大学,2009.
[75] 陈学习,吴立新,车德福,等. 基于钻孔数据的含断层地质体三维建模方法[J]. 煤田地质与勘探,2005,33(5):5-8.
[76] Meersmans J, van Wesemael B, De Ridder F, et al. Modelling the three-dimensional spatial distribution of soil organic carbon (SOC) at the regional scale (Flanders, Belgium)[J]. Geoderma, 2009, 152(1/2): 43-52.
[77] Taghizadeh-Mehrjardi R, Nabiollahi K, Kerry R. Digital mapping of soil organic carbon at multiple depths using different data mining techniques in Baneh Region, Iran[J]. Geoderma, 2016, 266: 98-110.
[78] Heitkamp F, Ahrends B, Evers J, et al. Spatial 3D mapping of forest soil carbon stocks in Hesse, Germany[J]. Journal of Plant Nutrition and Soil Science, 2021, 184(6): 635-656.
[79] 熊祖强,贺怀建,夏艳华. 基于TIN的三维地层建模及可视化技术研究[J]. 岩土力学,2007,28(9):1954-1958.
[80] 黄键初. 基于土壤-景观关系的土壤发生层三维建模方法研究[D]. 南京:南京师范大学,2022.
[81] 朱阿兴,闾国年,周成虎,等. 地理相似性:地理学的第三定律?[J]. 地球信息科学学报,2020,22(4):673-679.
[82] Shen Y G, Li A B, Huang J C, et al. Three-dimensional modeling of loose layers based on stratum development law[J]. Open Geosciences, 2022, 14(1): 1480-1500.
[83] 屈红刚,潘懋,王勇,等. 基于含拓扑剖面的三维地质建模[J]. 北京大学学报(自然科学版),2006,42(6):717-723.
[84] Wang B, Wu L, Li W J, et al. A semi-automatic approach for generating geological profiles by integrating multi-source data[J]. Ore Geology Reviews, 2021, 134: 104190.
[85] Mallet J L. Geomodeling[M]. New York: Oxford University Press, 2002.
[86] 郭甲腾,吴立新,周文辉. 基于径向基函数曲面的矿体隐式自动三维建模方法[J]. 煤炭学报,2016,41(8):2130-2135.
[87] 史舟,徐冬云,滕洪芬,等. 土壤星地传感技术现状与发展趋势[J]. 地理科学进展,2018,37(1):79-92.
转载请注明来自:http://www.lunwencheng.com/lunwen/lig/22677.html